Introduction
This article will introduce Tesla’s decision and planning module, Planner, which was discussed on AI Day.
Like a human driver, Planner receives 3D vector space processed by visual neural network and searches for a trajectory in that space to maximize the safety, comfort, and efficiency of the vehicle to reach the destination.
As an early adopter of autonomous driving, Tesla’s Planner is already capable of performing well in highway or city fast lane planning, including single lane keeping, navigation lane changing, active overtaking, automatic ramp up and down, all of which have been tested in mass production.
With the development of autonomous driving, the use of Tesla Autopilot needs to expand from highways to city roads, and Planner is expected to perform well in urban driving.
The complexity of urban autonomous driving requires the resolution of non-convex and high-dimensional problems in the decision and planning module.
Non-Convex Optimization
What is a “non-convex problem”?
This is an important data concept, referring to a local optimal solution that is not necessarily the global optimal solution in non-convex optimization problems due to the complexity of multi-peaked functions. Therefore, seeking optimal solutions in non-convex functions is much more challenging.
So, what is the relationship between this and autonomous driving?
We should know that the ultimate goal of autonomous driving is to compute the “optimal path” that satisfies constraints.
Simply, the algorithm itself is a mathematical optimization process, with the planning problem of autonomous driving being a “convex optimization problem,” and the avoidance constraint of autonomous driving is not a convex space. Moreover, autonomous driving safety cannot be achieved by only ensuring local safety, but rather, it must be ensured globally.
In summary, the “static + dynamic” constraint space for autonomous driving is a non-convex problem.
Why talk about convex optimization?
Convex optimization is currently the simplest nonlinear optimization method, or we could say, it is the only nonlinear optimization method that humans currently understand.- Convex optimization is the cornerstone of complex optimization methods, and most problems are transformed into convex optimization problems to be solved.

Non-convex problems can have multiple possible solutions, and they are relatively independent, but it is difficult to obtain a global optimal solution when searching. Planner is prone to entering local optima when searching.
High dimension:
The emergence of high-dimensional trajectory planning is because the car needs to plan the next 10 to 15 seconds and generate the position, velocity, and acceleration of the entire planning window’s ego vehicle. Generating a large number of parameters at runtime is required.
There are two commonly used methods to solve the above problems: discrete search methods and continuous function optimization.
Discrete search methods are very suitable for solving non-convex problems because they do not get stuck in local minima. But it performs poorly in solving high-dimensional problems because it is discrete and does not use any gradient information. Actually, exploring each point is necessary to know its cost, which is very inefficient.
Continuous function optimization is good at solving high-dimensional problems because they use gradient-based methods to quickly find a good solution, but for non-convex problems, they are prone to getting stuck in local minima, resulting in poorer solutions.
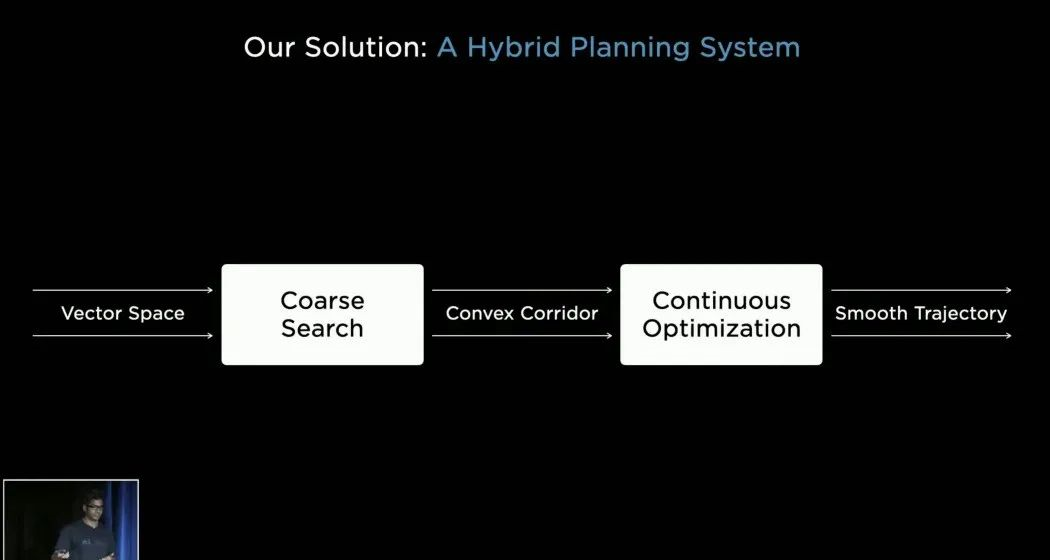
The solution from Tesla’s Planning and Control team is hierarchical decomposition, which is similar to Apollo’s planning algorithm.
First, use a coarse search method to decompose the non-convexity and transform the problem into convex space optimization, and then use an optimization algorithm to obtain the final smooth trajectory.
The following are two classic scenarios that introduce the processing flow of Tesla’s planning module:
Lane Change Planning
In this scenario, the request from the navigation node Routing module is that the ego vehicle needs to make a left turn at the second intersection ahead.
Therefore, the ego vehicle needs to change lanes to the left twice continuously to perform a left-turn operation at the second intersection. As shown in the figure above, Planner first found two feasible decisions when solving this problem.
- The first decision is to change lanes earlier, but due to the influence of obstacles ahead, the ego vehicle will undergo heavy braking, resulting in discomfort to passengers.
- The second decision is to change lanes in a farther place, and the speed planning result is to drive through the first intersection first and then change lanes.
Planner will perform thousands of such searches in a short time. In this scenario, 2500 searches will be performed within 1.5 ms, and the search speed is very fast.If the current speed is 60 km/h, the self-driving vehicle will only move forward 2.5 cm in 1.5 ms, but the Planner has assessed 2500 driving routes.
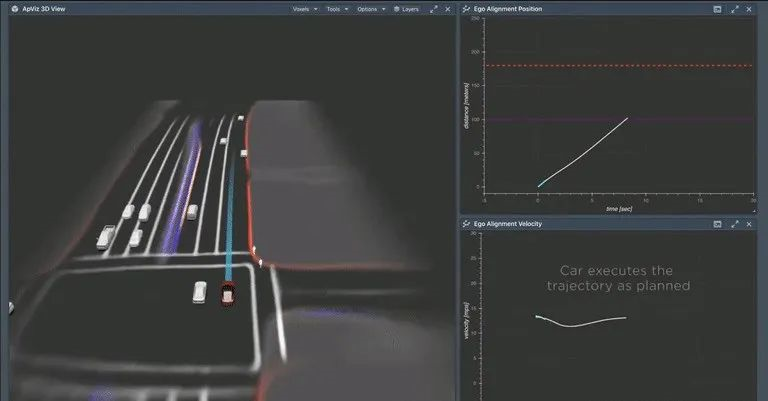
Ultimately, the Planner selects a smooth and safe optimal trajectory based on safety, comfort, and turning ease that aligns with the driver’s judgment.
Urban Road Planning Algorithm
We have examined Tesla’s planning algorithm’s performance on structured roads above, and now we will discuss how the Tesla planning algorithm performs on urban roads.
Compared with structured roads, urban roads are generally more complex, with not only a more complicated road structure but also more complex obstacle behavior, such as obstructed lane lines or obstacles.

In such scenarios, precise obstacle detection is crucial, and the planning algorithm must be better equipped to handle cars and pedestrians crossing the road. The algorithm must be optimized and robust.
The following example illustrates how Tesla’s planning algorithm handles complex urban environments:
When driving autonomously on urban streets (narrow roads), it is essential to anticipate barriers and adjust the vehicle’s decision-making behavior based on the projected trajectory for each object.
To accomplish this, the Tesla planning algorithm establishes the concept of independently planning the interaction with each obstacle.
In the scenario described earlier:
First, the oncoming Car 1 reaches the vehicle, and Autopilot slows down slightly. However, it realizes that it cannot avoid the oncoming car actively since there is no space on one side of the car. Instead, Car 1 can give way for us.
Autopilot continues to plan the forward route instead of blindly braking here. It is confident that Car 1 is driving slowly enough to parallel park and can make way for us.
Second, Car #2 approaches from the opposite direction at a higher speed. In this scenario, the Tesla decision planning algorithm plans the trajectory of another object.
The prediction results for the oncoming car:
- High probability: bypass other parked cars (red path)
- Low probability: Yield (green path)
Based on the prediction of Car 2’s trajectory, the self-driving algorithm decides to parallel park.Therefore, when the autonomous vehicle pulls over, we notice that if it chooses to concede based on the target obstacle’s lateral speed and acceleration, the autonomous driving algorithm changes its mind immediately and continues to move forward.
Remote Parking Problem
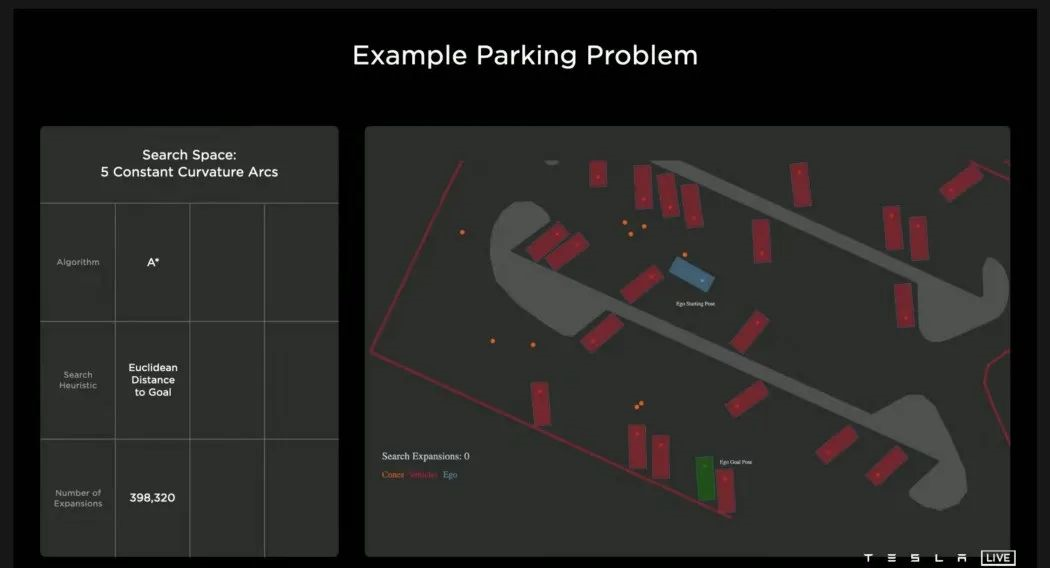
Discussing Tesla’s autonomous driving planning algorithm can actually start with Tesla’s intelligent parking. Most of the time, people think that solving autonomous driving on public roads is more difficult than solving autonomous driving in a limited scenario.
Obviously, this view is not correct. Parking for the last kilometer for Tesla is not that simple. Compared with public roads, this scenario needs to solve no less problems.
For Tesla, the parking scenario is actually consistent with the goal of public roads, which is to achieve high-level automation of vehicles. The goal of the parking scenario is that the self-driving car (blue) needs to be parked in the green parking space, bypassing the cars and cones (orange) on the roadside.
Baseline
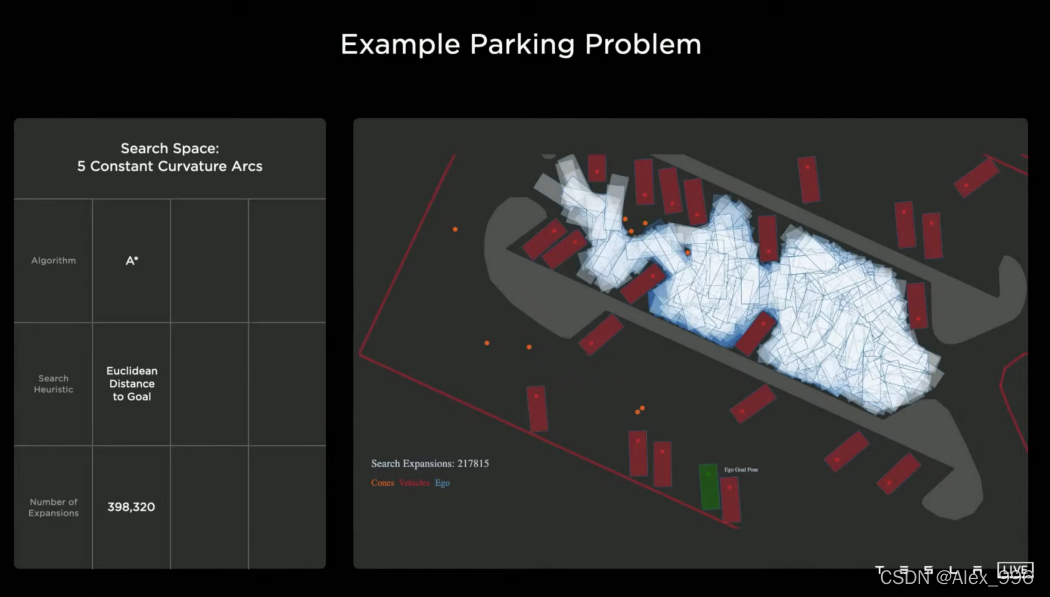
The simple baseline uses Algorithm A.
The heuristic function of A is the Euclidean distance, as you can see from the picture above, it quickly falls into a local minimum.
In the end, it made progress and reached the destination, but it used nearly 400,000 nodes to complete this operation.
Using Navigation
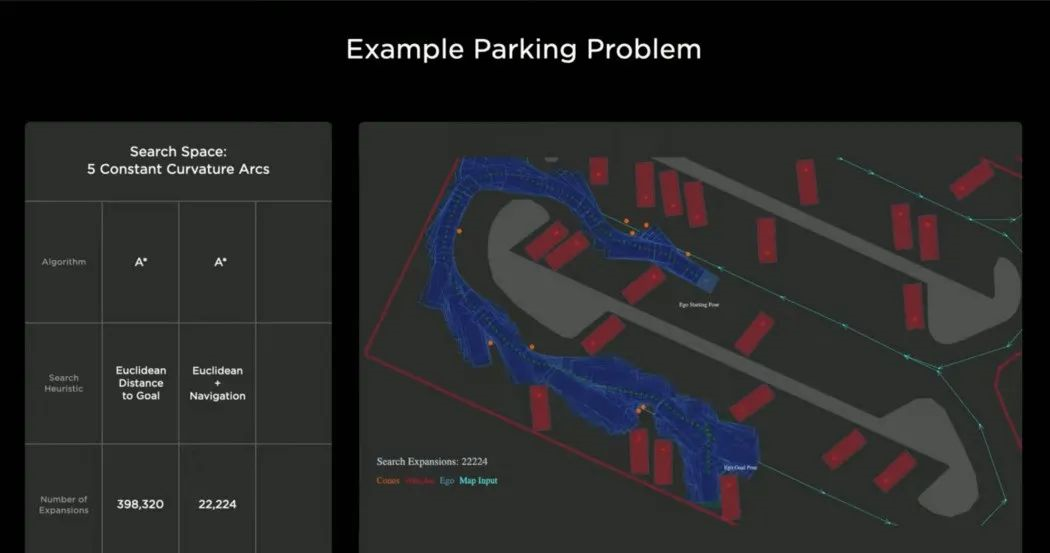
If a navigation route is added to the baseline, it will immediately help. But when encountering obstacles, it basically does the same thing as before, backtracking, and then searches for a brand new path. In the end, it still needs 22,000 nodes.
Monte Carlo Tree Search
Is there a more efficient solution?
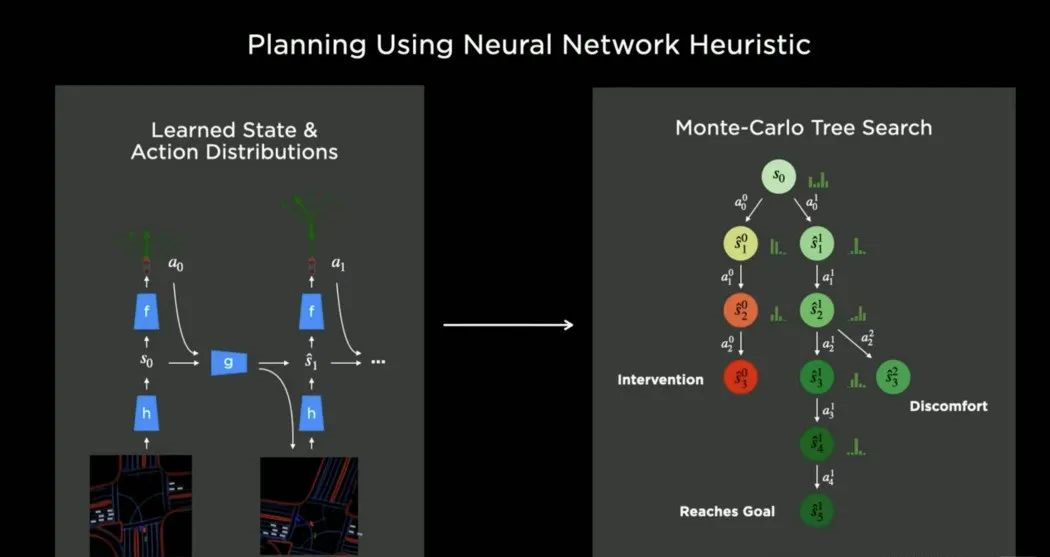
It’s time for “first principle thinking” again. Currently, the best practice for decision-making processes is to use heuristic search algorithms, and the best practice for heuristic search algorithms is Monte Carlo Tree Search (MCTS).
As of 2021, the best and latest algorithm based on MCTS is MuZero from DeepMind.
And what is DeepMind?
Take a look at the introduction on Baidu Baike:>DeepMind is a cutting-edge AI company under Google, co-founded by artificial intelligence programmer and neuroscientist Demis Hassabis, located in London, UK.
>
It combines the most advanced technology of machine learning and systematic neuroscience to establish powerful universal learning algorithms.
Interestingly, Andrej Karpathy had an internship experience there.
MuZero excels in playing Go, Chess, Shogi, and Atari without being informed of the rules.
It has the ability to devise a winning strategy in an unknown environment, which seems to be the perfect solution to Tesla’s parking problem, simply by turning the planning problem of self-driving into a “parking game”.
MuZero is a model-based planning system as well as a model-based reinforcement learning system, aiming to solve this problem by learning the precise model of the environment dynamics and then using it for planning.
Therefore, the Tesla AI team is studying neural networks that can generate state and action distributions and then can be inserted into Monte Carlo tree search with various cost functions. These cost functions can be explicit cost functions such as distance, collision, comfort, crossing time, and intervention of actual manual driving events.
The result is that the planner can basically move toward the goal once, even without using navigation heuristics, only given the scenario, the planner can directly move toward the goal.
The neural network can absorb the global context of the scene and then produce a value function that effectively guides it toward global minima rather than getting stuck in any local minima, with only 288 nodes needed.
So we must admire Tesla’s engineering capability. While more people are still discussing what else AlphoZero and MuZero can do besides playing games, Tesla has applied them to self-driving systems.
Final Words
Through Tesla’s introduction, we can find that the execution logic of decision-making and planning algorithms is very similar to that of human drivers. Not only is it a simple optimization problem, but more often, when solving trajectories, it involves predicting target obstacles and playing games based on predicted results, which can make the efficiency of peers higher and the entire self-driving process more intelligent.
Tesla’s algorithm does have its merits, but many new forces and self-driving companies in China currently have in-depth practice and technological accumulation in the field of autonomous driving algorithms for urban work conditions, and have achieved good results in some public tests. We should also have confidence in our domestic self-driving technology.
This article is a translation by ChatGPT of a Chinese report from 42HOW. If you have any questions about it, please email bd@42how.com.
