Editor’s note: In recent years, model predictive control (MPC) theory based on vehicle kinematic and dynamic models has been widely applied to autonomous vehicle control. MPC solves the optimization problem through rolling optimization based on pre-set system models and control inputs. The main advantage of MPC is that it can systematically handle multiple optimization targets and input/output constraints. In this study, an inverse optimal control (IOC) algorithm is proposed to learn the cost function from human demonstration data and apply the learned cost function to path-tracking MPC. The results show that the controller not only follows the reference trajectory but also makes lateral velocity, lateral acceleration, and other features closer to human driving.
Abstract: Path-tracking controllers play an important role in improving the dynamic behavior of autonomous vehicles. Model predictive control (MPC) is one of the most powerful controllers, which can handle multiple optimization targets and adapt to physical limits of actuators and vehicle states to ensure safety and other desired behaviors. As a high-potential solution, the human-demonstrated learning cost function can be integrated into MPC. By learning the cost function from human demonstration, it can avoid a large number of parameter adjustments and, more importantly, can adjust the controller to provide more natural control actions for humans. In this study, an innovative inverse optimal control (IOC) algorithm is proposed to learn the appropriate cost function for the control task from data collected from human demonstration. The goal is to design a controller whose generated motion matches specific features of human-generated motion, including lateral acceleration, lateral velocity, and deviation from the lane center. The results show that the designed controller can learn the desired features of human driving and achieve them while generating appropriate control actions.
Keywords: Autonomous vehicle, path-tracking controller, model predictive control, inverse optimal control
Introduction
Model predictive control (MPC) is considered as a suitable framework for designing path-tracking controllers for autonomous vehicles. This technique solves an optimization problem at each time step and can handle multiple objectives simultaneously. Moreover, it can adapt to physical limits of actuators and vehicle states to ensure safety and other required behaviors. In order to develop effective model predictive control for autonomous vehicles, an appropriate cost function should be defined. The design of cost functions often depends on the designer’s experience and proficiency. When passenger comfort is considered in the vehicle performance, the design of cost functions becomes much more complicated.
From an objective perspective, improving the control behavior of autonomous vehicles can enhance human comfort and safety [1], [2]. This consideration is a supplement to traditional vehicle ride comfort, which mainly depends on the vibration characteristics of the vehicle [3]-[5]. From a subjective perspective, comfort depends on human feelings and is difficult to express as a set of cost functions. Learning the cost function from human demonstration has been an attractive option for researchers as a high-potential solution.To study the cost function or some of its parameters, researchers have proposed Inverse Optimal Control (IOC). In this approach, expert demonstrations are often used as optimal control solutions for problems with unknown cost functions [6]. Considering the MPC problem under the context of IOC, the demonstration input can be viewed as an optimal input sequence for unknown cost function parameters. The optimal conditions for parameter control were initially outlined given demonstration data and cost function parameters. In addition, the IOC problem can be defined as a search algorithm to find suitable parameter values that satisfy the optimal conditions [7].
Another method to estimate the cost function from demonstrations is to use Inverse Reinforcement Learning (IRL). In some cases, IOC and IRL are interchangeably defined as the same method. In the context of IRL, probability methods such as Markov Decision Processes (MDP) are used to extract reward functions from proven optimal behaviors [8], [9]. In the MDP method, particularly for the case of Reinforcement Learning (RL), it is assumed that the cost function is known. However, as mentioned earlier, designing an appropriate cost function for RL is also challenging. IRL has been used for imitation learning (sometimes called apprenticeship learning) with the goal of finding a control policy that performs as well as the demonstrator in the absence of knowledge of the reward function [9].
IRL and IOC have been proposed for many different types of systems, such as humanoid robots [10], helicopter control [11], and replication of specific driving styles [12]. In [10], IRL was proposed to find a reward function to design more natural and dynamic running behavior for humanoid robots using data from human demonstrations. From the simulation results, the learned reward function showed good generalization properties that can be used in different environments. Even if the optimization problem was solved offline, the learned reward function could be easily integrated into an online MPC algorithm. Similarly, in [13], IOC was implemented for humanoid motion control. However, in this case, joint motion was not considered; instead, the position and orientation of the humanoid robot were used to describe motion using a two-layer optimization problem. The weight of the cost function was iteratively controlled and attempted to minimize the distance between the measured data and the solution obtained from the optimal control collected from the low-level control.Under the background of autonomous driving, IRL has been proposed to predict human intentions. For example, it is used to model human behavior and infer human driver’s route preferences [14]. Similarly, in [15], IRL is used to predict drivers’ intentions on the road. The motion of human drivers is formulated as an optimization problem and IRL is used to find the reward function. In [12], IRL is also used to replicate individual driving styles when generating trajectories followed by autonomous vehicles. In this work, maximum entropy IRL [14] is used to solve the path planning problem for autonomous driving. Additionally, the cost function is approximated as a linear combination of features in a similar way as [9]. The ultimate goal of IRL is to find suitable weights for each feature of the cost function, which is used to generate optimized trajectories for vehicles.
Although IOC and IRL have been implemented for various applications mentioned above, to our knowledge, these techniques have not been used for path tracking controllers of autonomous vehicles. Considering that improving the vehicle’s handling performance can improve passenger comfort, a learning-based MPC based on human-demonstration data may be feasible to adapt to this measure and improve passenger comfort. In this paper, we propose to use IOC for learning-based MPC for the path tracking task of autonomous vehicles. To achieve this, a novel feature-based MPC parameter cost function is designed. Furthermore, an innovative IOC algorithm is proposed to learn the appropriate cost function parameters of MPC using data collected from human demonstrations. The data is collected using the integrated 3D simulation environment “Unreal Engine” and Matlab-Simulink platform. The goal is to design a controller that produces motion matching specific features of human-generated motion, including lateral acceleration, lateral velocity, distance from the lane center, and yaw rate. The cost function parameters are learned from human demonstration data. These parameters are then used to implement the MPC controller for autonomous vehicles.
The rest of this paper is organized as follows. In section Ⅱ, the theoretical framework behind learning cost functions from human demonstrations is introduced. The formulation of MPC, the definition of cost function, and the methodology of IOC are explained in detail. Section Ⅲ outlines the experiments of collecting data from human demonstrations, the steps taken to learn the cost function from collected data, and the application of learned parameters in the path tracking controller. In sections Ⅳ and Ⅴ, the results are presented and further discussed, and the conclusion of the study is given.
Learning Cost Functions from Human DemonstrationsThe main objective of this work is to find an appropriate cost function for path tracking tasks using data collected from manual demonstrations. Road profile significantly affects the control behavior of autonomous vehicles [16], and in this work, the trajectory of manual demonstrations is considered as the best solution for a given reference path. Additionally, it is assumed that there exists a cost function associated with the trajectories generated by human drivers. The goal is to find appropriate parameters for the cost function that capture selected features of individual human driving tasks. In this section, the formula for the MPC controller is first discussed, followed by the design of a feature-based MPC cost function. Finally, the design of IOC is elaborated.
A. Model Predictive Control
In MPC, the future state of the vehicle within a specific range is calculated based on the vehicle’s transition model. At each time step, a nonlinear optimization problem is solved to generate control actions that minimize the cost function. In the optimized control sequence, only the first control action is sent to the vehicle, and the entire process is repeated within the next time interval. One of the main advantages of the MPC controller is that it can handle multiple objectives. Additionally, since it solves a constrained optimization problem, it can constrain the vehicle’s state (e.g., steering angle) to match physical limitations. For this work, the vehicle state χ=[X,Y,ψ,vy, r, ay] and the steering angle input u=δ are considered, where X and Y are the vehicle’s position in the global coordinate system, ψ is the heading angle, r is the yaw rate, vy is the longitudinal speed, and ay is the longitudinal acceleration. For these vehicle states and steering angle inputs, the vehicle transition model can be represented as:
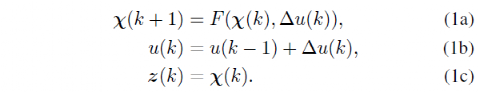
The cost function of the learning-based controller can be represented in parameter form and updated to improve the controller’s performance, i.e., to mimic manual demonstrations. The MPC problem with a parameterized cost function can be represented as:
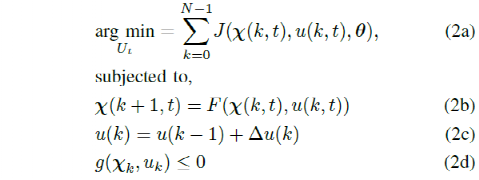
where g(χk,uk) represents state and input constraints, and θ represents the parameter vector of the cost function. By solving this optimization problem, an optimized control sequence U* = [uk….uk+N] is found, and only the first control action of the sequence is sent to the vehicle at each time step. This process is repeated within the next time interval.
B. Cost Function
An improved autonomous vehicle path tracking controller should adapt to accurate and safe path tracking while generating control actions that provide a more natural movement for humans. Parameterized cost functions are considered here, and feature-based learning techniques are used to find the best values of the parameters that produce features similar to those of human drivers. For each trajectory generated by manual demonstrations or the controller, the following features are used to design the parameterized cost function.a) Lane Center Distance: This feature represents the deviation between the vehicle and the lane center, and can be expressed as
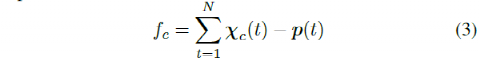
where t is the time, χc (t)=[X, Y] is the position of the vehicle on the road at time t, p (t)=[Xref, Yref] is the road point closest to the vehicle’s position, N is the number of samples in the trajectory.
b) Deviation Angle from Path: This feature represents the deviation between the vehicle’s lateral angle and the path angle.
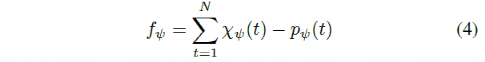
where χψ is the vehicle’s heading angle and pψ is the path angle.
c) Lateral Velocity: Another feature that needs to be compared with human driving is the vehicle’s lateral velocity, which is expressed as
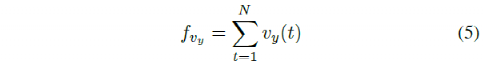
d) Yaw Rate: Yaw rate is an important feature that affects passenger comfort for path tracking tasks. This feature can be calculated as
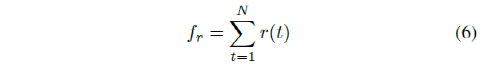
e) Lateral Acceleration: One of the most important features that significantly affects passenger comfort is the vehicle’s lateral acceleration, which is calculated as
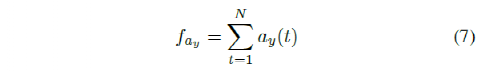
Finally, using these features, the cost function for path tracking tasks is expressed as
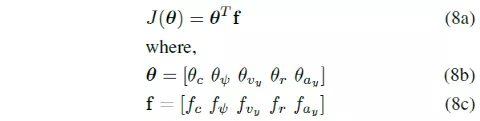
where θ is the parameter or weight vector that needs to be learned from human demonstrations in order to match the motion generated by MPC with the features in human demonstrations.
C. Inverse Optimal Control
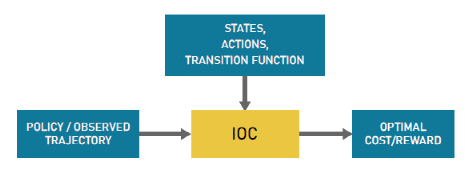
In general optimal control problems, the goal is to find control actions or policies based on certain criteria. These criteria are usually expressed using cost functions that provide the cost of choosing actions. However, designing an appropriate cost function is difficult and often requires a lot of time to adjust. In the IOC method, the goal is to find a suitable cost function based on user demonstrations instead of finding the optimal policy. Then, the cost function can be used to generate an optimal policy. Figure 1 shows a general schematic of the IOC process. IOC and IRL techniques can be used interchangeably since they describe similar methods.## Translate Chinese Markdown into English Markdown
As a translator in the automotive industry, my task is to translate the following Chinese Markdown text into professional English Markdown text, preserving the HTML tags within the Markdown. I will only output the corrected and improved parts of the translation, without writing explanations.
During this process, it is important to design an appropriate cost function that clarifies the design preferences and objectives. For example, adjusting different parameters of the cost function to obtain optimal performance for complex tasks such as autonomous driving is not simple. In this regard, IOC provides a suitable option to adjust the cost function based on data collected from manual demonstrations.
The manual demonstration dataset D consists of P trajectories used to consider various driving scenarios. Assuming the existence of a cost function related to human driving tasks, suitable weights can be found for the MPC controller to replicate some features of human driving motion. To achieve this, the driving task of humans is expressed using the characteristics discussed in II-B. For a set of unknown cost parameters, the expected features of manual demonstrations can be expressed as follows:
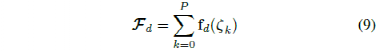
Here, the image is the feature vector of all demonstrations, fd is the feature vector of the demonstrated trajectory, and ζk is the k-th trajectory in the data set D. The goal is to find a set of cost parameters that match the expected features of the learned controller with those of the manual demonstration. The difference between the demonstrated features and controller features can be represented by the following gradient:
Here, fl is the feature vector of the trajectory generated by the controller for a fixed parameter value θ. Using the image, the optimization value θ* can be found by solving the gradient-based optimization method. However, calculating the expected feature of the learning system is not simple, especially for high-dimensional and complex systems like autonomous driving vehicles. When designing path tracking controllers for autonomous driving vehicles, we approximate the most likely trajectory as the solution to a nonlinear MPC problem with a given parameter set and use the trajectory generated by MPC to calculate the expected feature of the learning controller. Then, following the same process, adjusting the weight values based on the gradient image until convergence.
Model-Based Manual Demonstration and Implementation
In this section, data collected from manual demonstrations is explained, and the implementation of the proposed IOC method is also discussed.
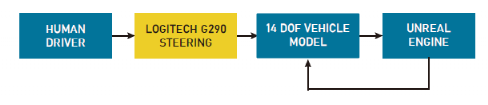
A. Manual Demonstration DataTo implement learning-based control methods, a simulator was used to collect human demonstration data. For vehicles, a nonlinear dynamic model can be used to effectively simulate their motion [17], [18]. A 14-degree-of-freedom vehicle dynamics model was used to capture the vehicle’s dynamic behavior. In addition, the 3D simulation environment “Unreal Engine” was used to render the environment. The vehicle model implementation and environmental simulation were both done in MATLAB-Simulink. The Logitech G290 steering pedal system was used to drive the vehicle in the simulation environment, while data was collected through communication between the Unreal Engine and the vehicle dynamics model. Figure 2 shows the software architecture of the data collection flow.
Data from 10 human drivers were collected to evaluate the effectiveness of the proposed method. Figure 3 shows snapshots of the hardware setup and environment rendering in the Unreal Engine. Initially, all drivers were required to familiarize themselves with the driving controller and environment to understand their reaction to the simulation environment. After driving for 10 minutes, drivers were required to drive in three specific road conditions while maintaining a speed between 30-35km/h. A selected path profile composed of different types of curves was used for each road, and each driver’s five attempts were recorded for each road. In the three driving scenarios, two scenarios were used to learn cost function parameters, and one scenario was used to test the controller’s performance.
B. Learning the Cost Function from Human Demonstrations
For the collected driver-specific dataset, the following formula was used to calculate the feature values:
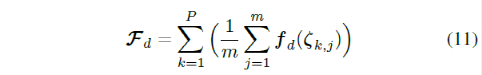
where m is the number of experiments for each driving scenario, and P is the total number of driving scenarios. For all driving scenarios, the reference position was the center of the lane. To learn the weight parameters θ, the vehicle was set as the starting point for each driving scenario. A randomly selected set of initial weight parameter (θ) values was then used to drive the vehicle on all roads using the MPC controller. After completing the driving scenario, the expected features of the trajectory generated by the controller were calculated using the following formula:
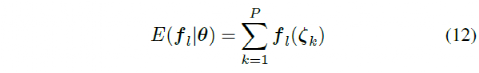
The optimized gradient based on the expected features of the controller and the human demonstration can be calculated as follows: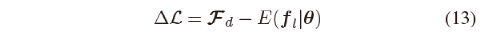
Use this gradient to update the value of θ and continue the process until convergence.
C. Trajectory Tracking Controller
The learning weights found from the IOC algorithm are used in the cost function of MPC to perform the path tracking task for autonomous driving vehicles. The MPC formula described in section II-A is used to simulate the performance of the controller. More details on MPC implementation can be found in our previous work [19]. For the MPC controller, a prediction range of Np=5 and a control range of Np=5 are used. Nonlinear optimization problems are solved using the “Ipopt” package and open source optimization tool “CasAdi” [20].
Results and Discussion
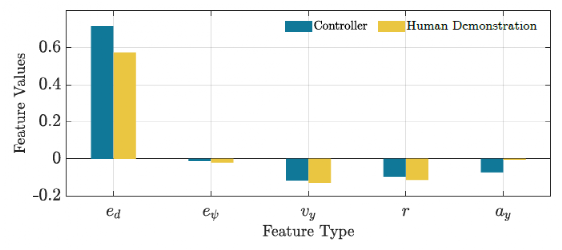
The weight parameters are learned from two driving scenarios. The third scenario is a test driving scenario used to evaluate the performance of the controller. Figure 4 shows the performance comparison of the controller and human driving in the training driving scenario when calculating features. Figure 5 shows the same comparison in the test driving scenario. As expected, the feature values in Figure 4 are closer to the corresponding human demonstrations. From the results in Figure 5, the learned controller shows appropriate generalization ability, so it can be used in other environments. Figure 6 depicts a comparison of the human driving trajectory and the trajectory generated by the learned controller for the test driving scenario. From this figure, it can be seen that the learned controller is not only able to follow the reference trajectory, but also able to learn the required features of human driving and implement them while generating appropriate control actions.
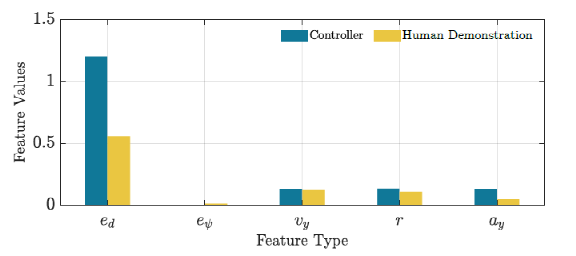
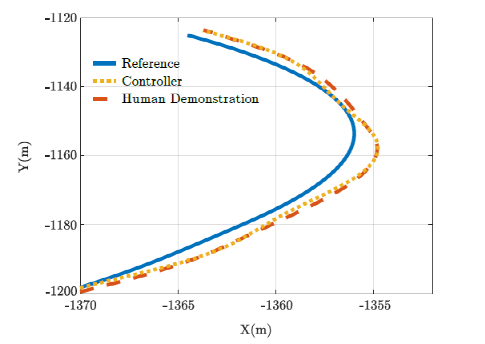We made several assumptions in our preliminary study on learning-based MPC. Firstly, the forward velocity was kept within a small range of 30-35 km/h, which was demonstrated by humans. Data collected for training did not consider scenarios where the velocity was less than 30 km/h. Similarly, in order to learn the weights, the vehicle’s velocity was kept constant at the average velocity of the human demonstrations for each specific driving scenario. Additionally, training and testing scenarios only included paths with different curvatures. Our future plan is to conduct more rigorous training to evaluate the generalization ability of the learning controller using this method.
Summary
Model Predictive Control (MPC) is an effective control technique for designing path tracking controllers for autonomous vehicles. This technique implements an optimization step that can handle multiple objectives and adapt to physical constraints of the actuators and vehicle states to ensure safety and other desired behaviors. Learning the cost function from human demonstrations is considered an attractive choice to avoid extensive parameter tuning for MPC. Most importantly, it allows the controller to adjust to provide more natural control actions for humans. Inverse Optimal Control (IOC) and Inverse Reinforcement Learning (IRL) schemes have been proposed to learn the cost function or some parameters of the cost function.
In this paper, we propose an innovative IOC algorithm to learn a suitable cost function for the control task using data collected from human demonstrations. The goal is to design a controller that generates motions matching specific features of human-generated motions. These features include lateral acceleration, lateral velocity, distance from the lane center, and yaw rate. To achieve this, the cost function’s parameters are learned from the human demonstrations data. Then, these parameters are used to implement an MPC controller for path tracking of autonomous vehicles. The performance comparison between the controller and human driving for computing the features is demonstrated for training and testing driving scenarios. As expected, the feature values in the training scenarios are closer to the corresponding human demonstrations. The learned controller exhibits proper generalization abilities and can be used in different environments. It is also observed that the learned controller can not only learn the desired features of human driving but also follow the reference trajectory. The future plan is to conduct more rigorous training with actual driving scenarios and enhance the generalization ability of the learning controller.
Translated from: “Learning-based Model Predictive Control for Path Tracking Control of Autonomous Vehicle”
Source: 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC)
Authors: Mohammad Rokonuzzaman, Navid Mohajer, Saeid Nahavandi, Shady Mohamed
This article is a translation by ChatGPT of a Chinese report from 42HOW. If you have any questions about it, please email bd@42how.com.